Speed of algorithms (with cats)

Let's see how programmers evaluate fast and slow algorithms. Since the topic is pretty boring, we'll use silly cat examples.

Constant time: O(1)

This is your best option. The algorithm speed does not depend on the number of cats.

🐾 Example

You are the lucky owner of N cats. Every kitten knows their name. If you call "Felix!", only one will come running, and the rest of the N-1 fluffs don't care.

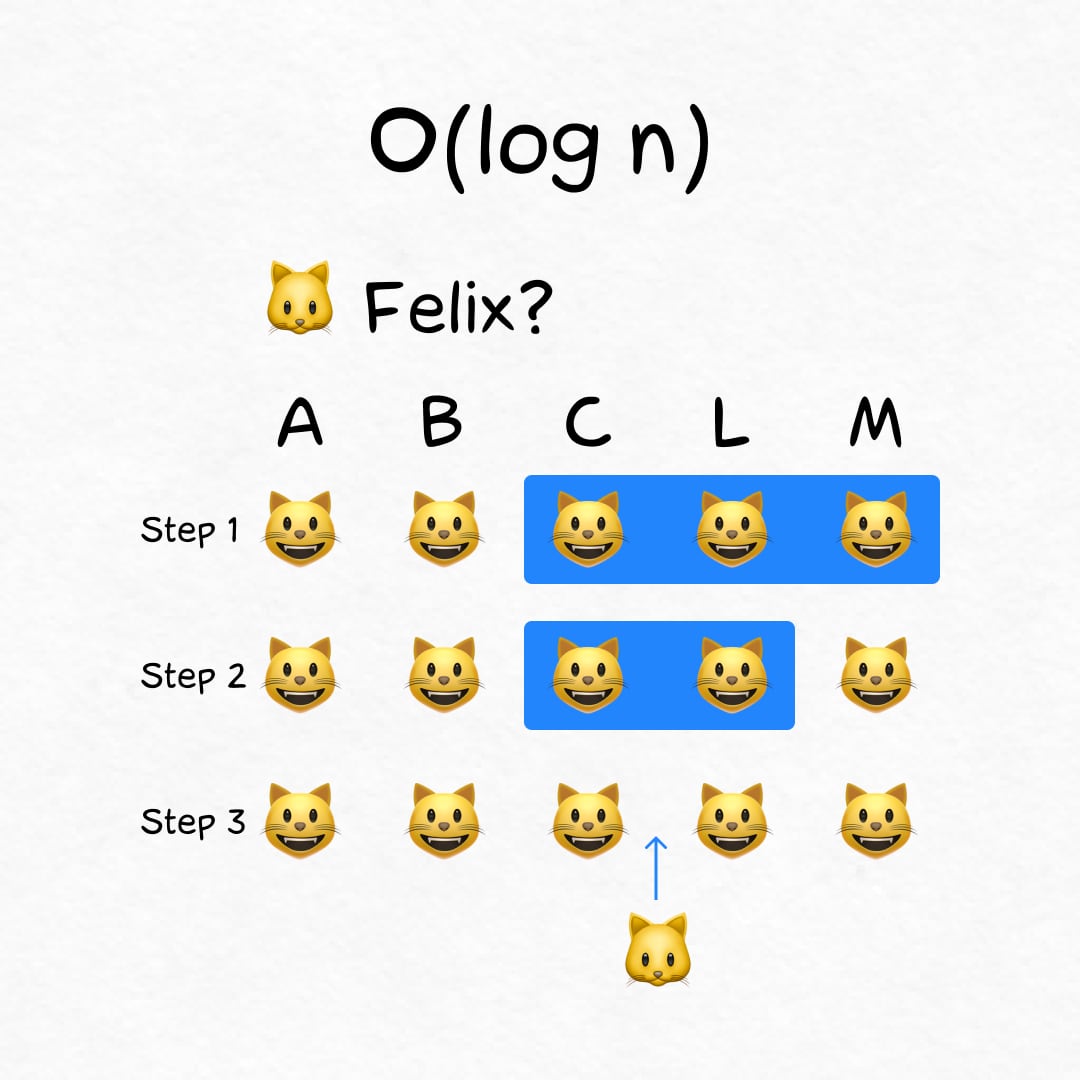
Logarithmic time: O(log n)

On N cats the algorithm completes in log(N) steps. It's fast! 1,000,000 kittens → 20 operations total.

🐾 Example

Cat's bowls are arranged alphabetically. When you adopt a new cat, the place for its bowl can be found in log(N) steps.

Linear time: O(n)

On N cats the algorithm completes in N steps. It means that every time you have to traverse all cats. Not great, not terrible.

🐾 Example

Your kittens rebelled and stopped responding to nicknames. Now you have to look through N fluffs to find the right one.

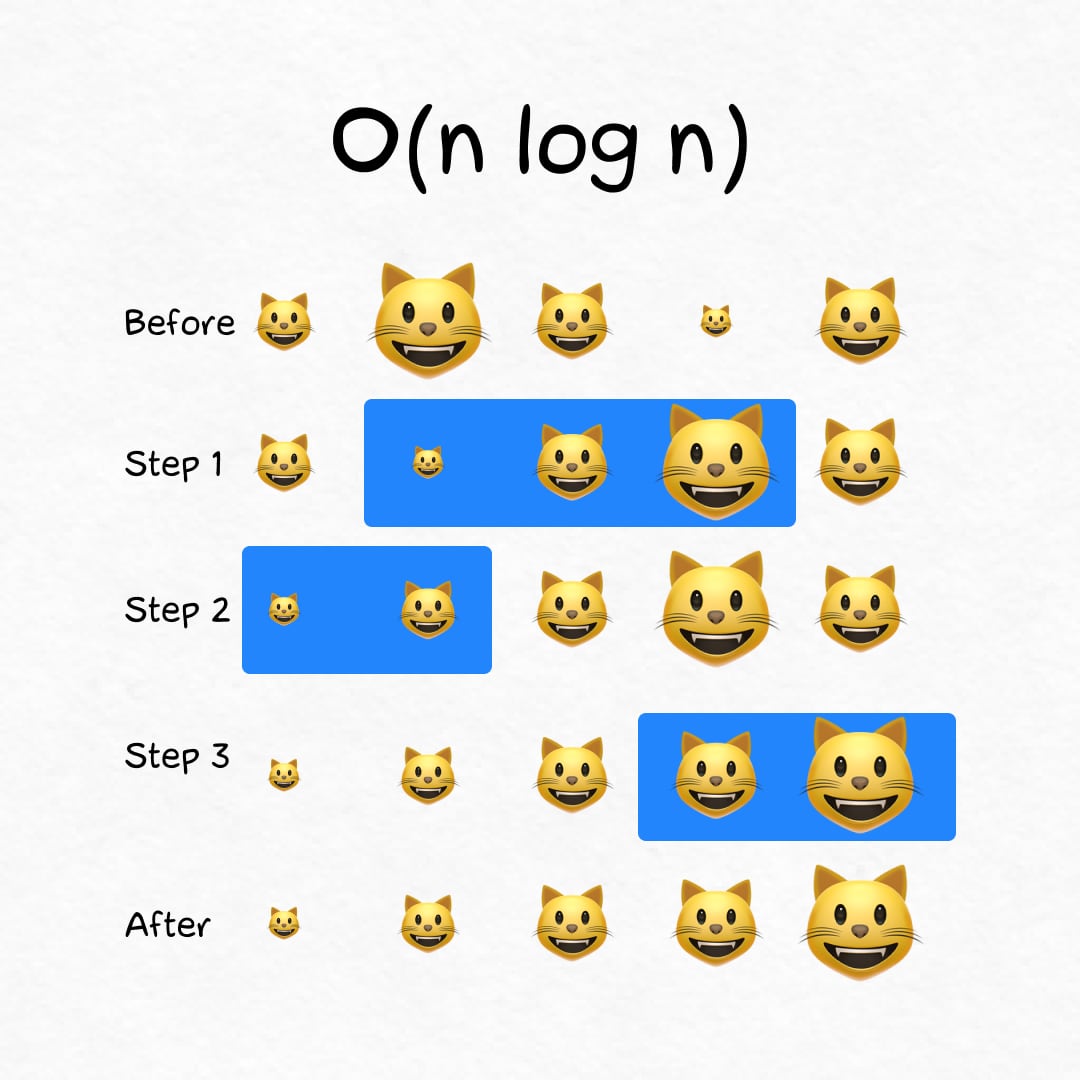
Log-linear time: O(n log n)

On N cats the algorithm completes in N × log(N) steps. This is slower than in linear time, but not by much (the logarithm of N is much smaller than N, remember?).

🐾 Example

Waiting for guests, you decided to seat kittens in the order of their size. The quick sort algorithm will handle this in N × log(N) steps.

Next in line, we have lazy polynomial cats and snail-speed superpolynomial ones.

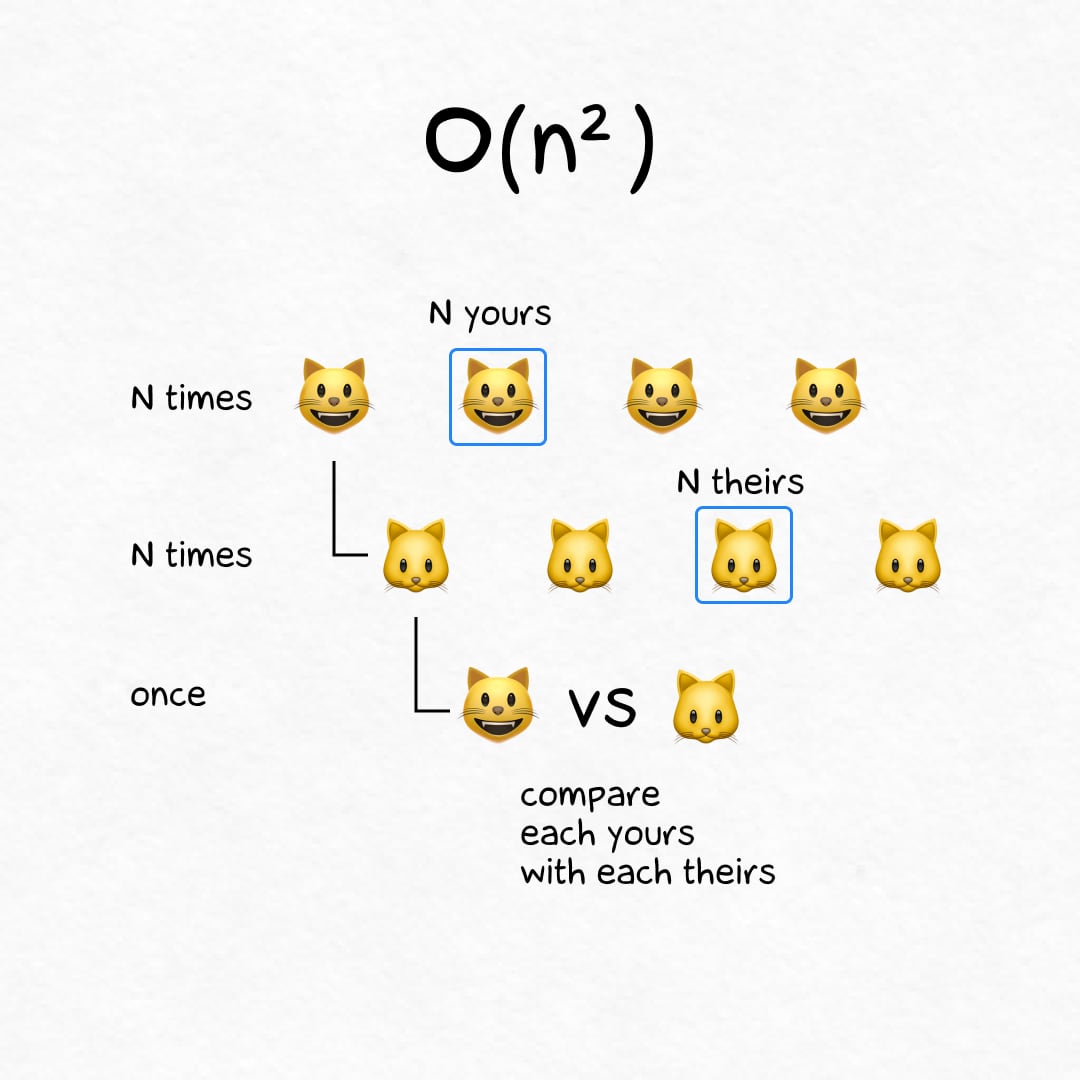
Quadratic time: O(n²)

On N cats the algorithm completes in N² steps. So slow.

🐾 Example

Your competitor claims that his N kittens are smoother and happier than yours. A special commission will compare the cats in pairs and make a fair verdict. You will need ~ N² comparisons.

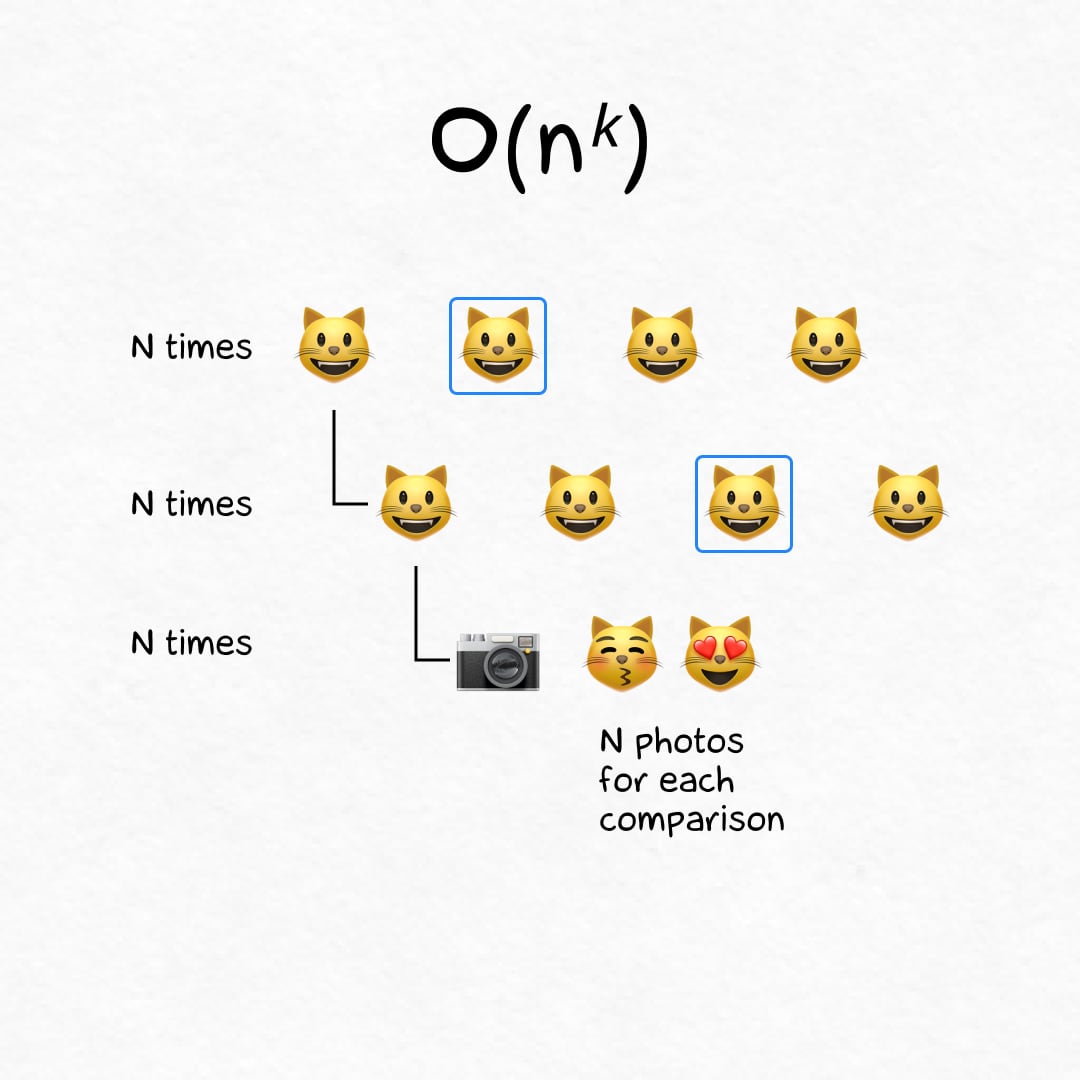
Polynomial time: O(nᵏ)

On N cats the algorithm completes in N³ steps, N⁴ steps, N⁵ steps, or even longer. Ugh. Don't be like that.

🐾 Example

Photoshoot! Each of the N kittens will be photographed in pairs with others, and the photographer takes N pictures for each pair. N × N × N ≃ N³ steps.

Polynomial algorithms are not famous for their speed. But compared to superpolynomial ones, they are as fast as a Flash. Sadly, the only "super" part of superpolynomial algorithms is a name. Let me show you.

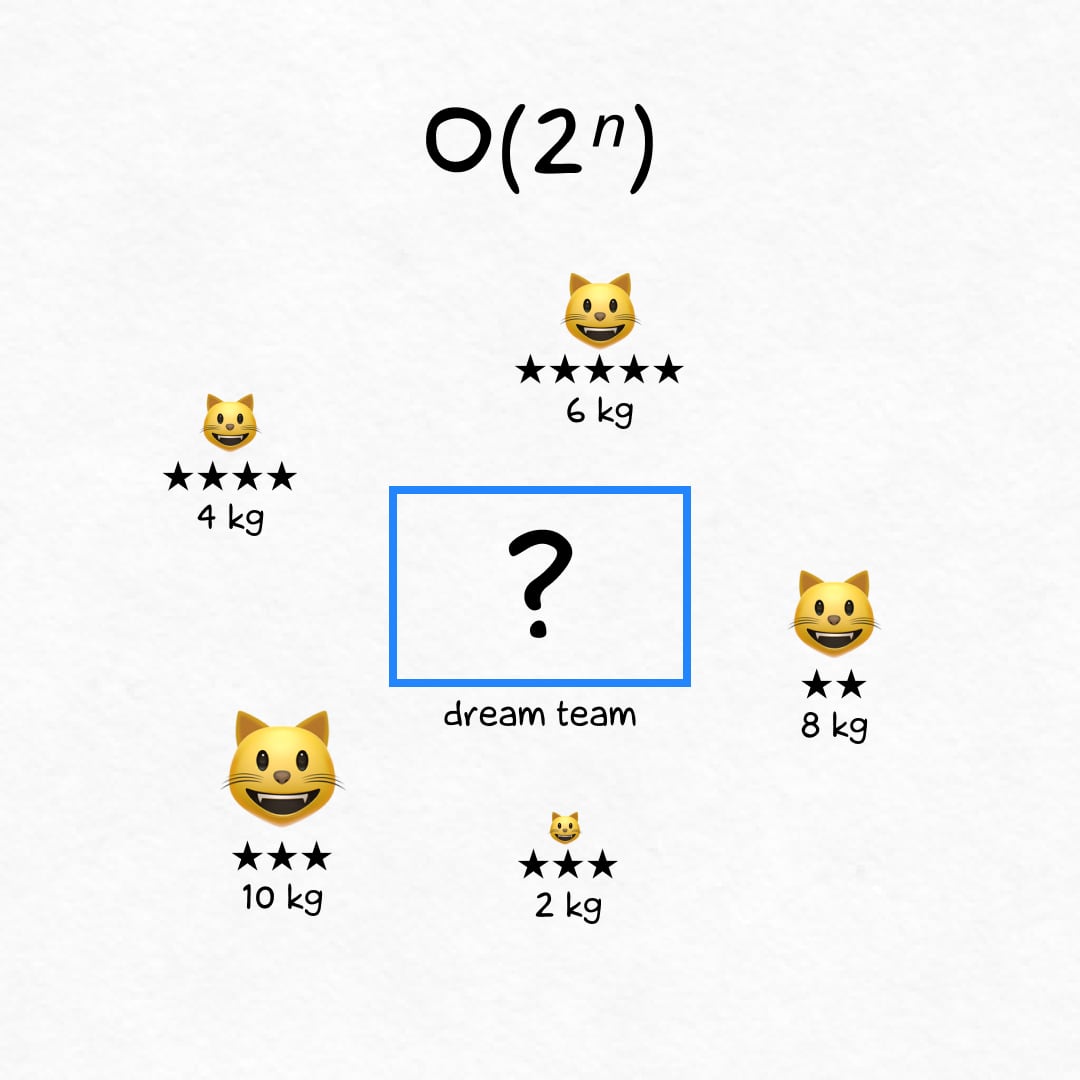
Exponential time: O(2ⁿ)

On N cats the algorithm completes in 2ⁿ steps. It's a long time, you're probably not gonna wait.

🐾 Example

Kittens are going to the cat show. Everyone will be weighed and rated in stars. But the cat transport can handle a maximum of X kilograms (or pounds). How to choose the most stellar cast? The answer will require 2ⁿ steps.

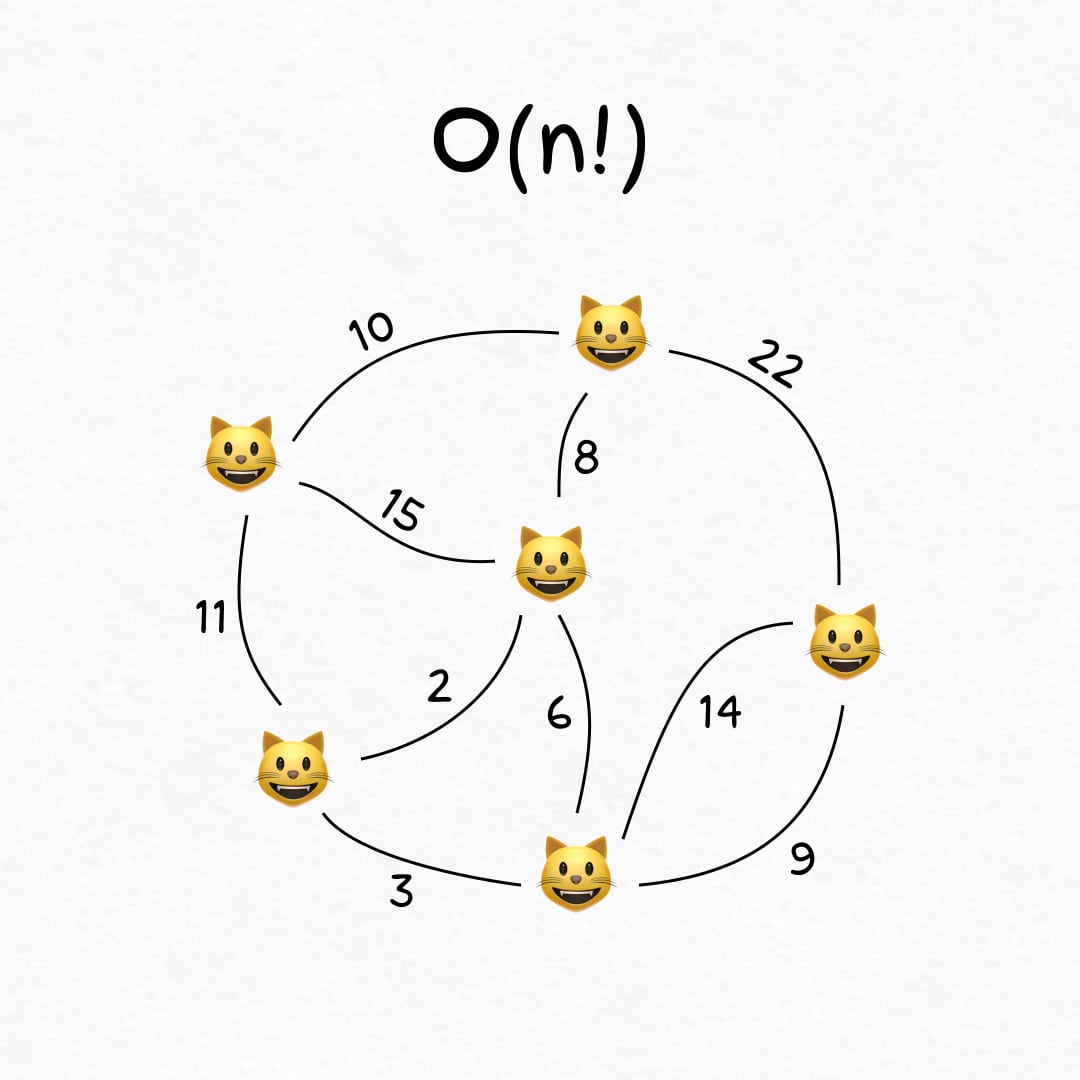
Factorial time: O(n!)

On N cats the algorithm completes in N ×(N-1) ×(N-2) ×... × 1 steps. This is crazy! With 20 cats it's already a couple of quintillion operations.

🐾 Example

Kittens spread out across the apartment. You want to pet everyone, but you're lazy and don't like walking. What is the shortest route to visit all fluffs? This is ~ N! comparisons.

Summary

Here are the algorithms we've covered:

Constant O(1)
Logarithmic O(log n)
Linear O(n)
Log-Linear O(n log n)
Quadratic O(n²)
Polynomial O(nᵏ)
Exponential O(2ⁿ)
Factorial O(n!)

A constant algorithm is always the best option, and a logarithmic one is almost always. Linear and polynomial ones are more complex — it all depends on the task with them. Sometimes it's a shame to choose O(n), and sometimes O(n²) is a huge success.

O(2ⁿ) and O(n!) are insanely slow. So in practice, people often use suboptimal but fast algorithms.

Subscribe to keep up with new posts.